NÚMEROS REALES
NUMEROS REALES
El conjunto de los números
reales pertenece en matemáticas a la recta numérica que comprende a los números
racionales y a los números irracionales. Esto quiere decir que incluyen a todos
los números positivos y negativos, el símbolo cero, y a los números que no
pueden ser expresados mediante fracciones de dos enteros que tengan como
denominador a números no nulos (excluye al denominador cero).
Un número es la expresión de
una cantidad con relación a su unidad. El término proviene del latín numeras y
hace referencia a un signo o un conjunto de signos. La teoría de los números
agrupa a estos signos en distintos grupos.
Los números naturales, por ejemplo,
incluyen al uno (1), dos (2), tres (3), cuatro (4), cinco (5), seis (6), siete
(7), ocho (8), nueve (9) y, por lo general, al cero (0).
SISTEMAS DE NUMEROS REALES
El sistema de números reales
se compone principalmente de dos grandes conjuntos, el de los números
racionales que son aquellos que pueden ser expresados como la división de dos
números enteros como 3434, 1515, incluso un número entero puede ser expresado
como una fracción, ya que el número entero puede ser dividido para 11 sin
cambiar su esencia, por ejemplo el número 88 puede ser expresado en fracción
así 8181; mientras que el otro gran conjunto del sistema de números reales es
el de los números irracionales cuya representación decimal es expansiva,
infinita y aperiódica.
OPERACIONES CON NÚMEROS REALES
Con números reales pueden
realizarse todo tipo de operaciones básicas con diversas excepciones
importantes:
No existen raíces de orden par
(cuadradas, cuartas, sextas, etc.) de números negativos en números reales,
(aunque sí existen en el conjunto de los números complejos donde dichas
operaciones sí están definidas).
La división entre cero no está
definida (pues cero no posee inverso multiplicativo, es decir, no existe número
x tal que 0·x=1).
No se puede hallar el
logaritmo de un número real negativo, cualquiera sea la base de logaritmos, un
número positivo distinto de 1.10
Estas restricciones tienen
repercusiones en otras áreas de las matemáticas como el cálculo: existen
asíntotas verticales en los lugares donde el denominador de una función racional
tiende a cero, es decir, en aquellos valores de la variable en los que se
presentaría una división entre cero, o no existe gráfica real en aquellos
valores de la variable en que resulten números negativos para raíces de orden
par, por mencionar un ejemplo de construcción de gráficas en geometría
analítica.
TIPOS DE NÚMEROS REALES
Racionales e irracionales
Un número real puede ser
un número racional o un número irracional. Los números racionales
son aquellos que pueden expresarse como el cociente de dos números enteros, tal
como 3/4, -21/3, 5, 0, 1/2, mientras que los irracionales son todos los demás.
Los números racionales también pueden describirse como aquellos cuya
representación decimal es eventualmente periódica, mientras que los
irracionales tienen una expansión decimal aperiódica:
Algebraicos y transcendentes
Otra forma de clasificar los
números reales es en algebraicos y trascendentes. Un número es algebraico si
existe un polinomio de coeficientes racionales que lo tiene por
raíz y es trascendente en caso contrario. Obviamente, todos los números
racionales son algebraicos: si es un número racional, con p entero
y q natural, entonces es raíz de la ecuación qx=p.
Sin embargo, no todos los números algebraicos son racionales.
Computables e irreductibles
Un número real se dice
computable si tiene una complejidad de Kolmogórov finita, es
decir, si puede escribirse un programa informático de extensión finita que
genere los dígitos de dicho número. Si un número real no es computable se dice
irreductible. Una definición de número irreductible es:
El conjunto de números reales
computables se designa por . Obviamente los racionales y los algebraicos
son números computables.
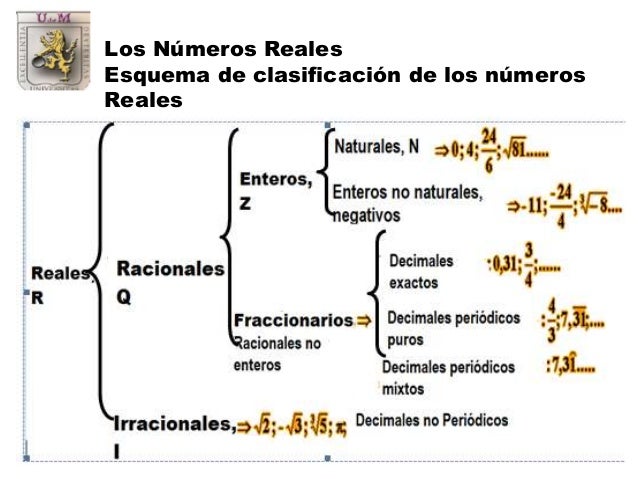
LOS NÚMEROS REALES SE CLASIFICAN EN:
Representación De Números
Reales
En la recta numérica, la
representación de números reales se puede hacer con una exactitud aproximada,
sin embargo, se pueden usar técnicas para representarlos de forma exacta. Como
en el siguiente ejemplo de 7–√7:
Allí se puede ver que la raíz
de 7 se puede descomponer para poder trazar un triángulo que cumpla con el
teorema de Pitágoras.
Primero se descompone 7 en suma de cuadrados:
7=22+(3–√)2

Comentarios
Publicar un comentario